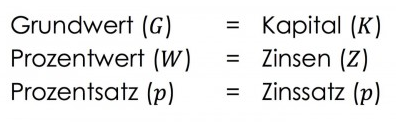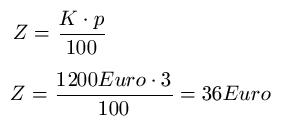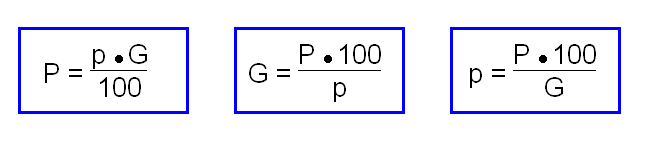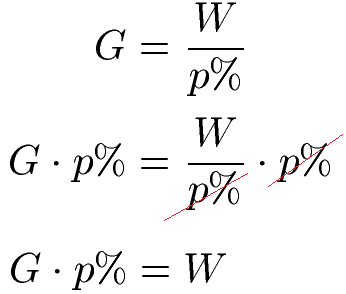Prozentrechnung Formel Einfach
Bei jeder für die prozentrechnung wichtige formel spielen sie eine rolle.

Prozentrechnung formel einfach. Eine alternative lösungsmethode ist das lösungsverfahren mittels dreisatz. In diesem artikel findet man die wichtigsten formeln mit erklärungen und beispielen. Was der grundwert der prozentrechnung ist und wie man diesen berechnet lernt ihr hier. P dfrac42 cdot 100700 6 antwort.
Grundlegend für die prozentrechnung sind in allen formeln die begriffe prozentsatz prozentwert und grundwert. Der prozentwert ist in dem fall der gesuchte wert. Ganz einfach ist es wenn man sich an folgende formel hält. Wir wollen also wissen wie viel 26 von 133 sind.
Die prozente geben hierbei das verhältnis zweier größen in hundertsteln an. Diese formeln werden manchmal in worten angegeben und in anderen fällen werden variablen buchstaben verwendet. Excel prozent die prozentrechnung ist in excel keine schwere sache. Prozentrechnen ist dein ständiger begleiter.
Für eine grundsätzliche anschauung zum prozentzeichen und seiner bedeutung siehe prozent. Dabei eine definition für den grundwert vorgestellt und es werden beispiele mit den formeln vorgerechnet. Dabei eine definition für den grundwert vorgestellt und es werden beispiele mit den formeln vorgerechnet. Prozentrechnung einfach erklärt 9 aufgaben mit lösung im folgenden wollen wir uns mit der prozentrechnung beschäftigen.
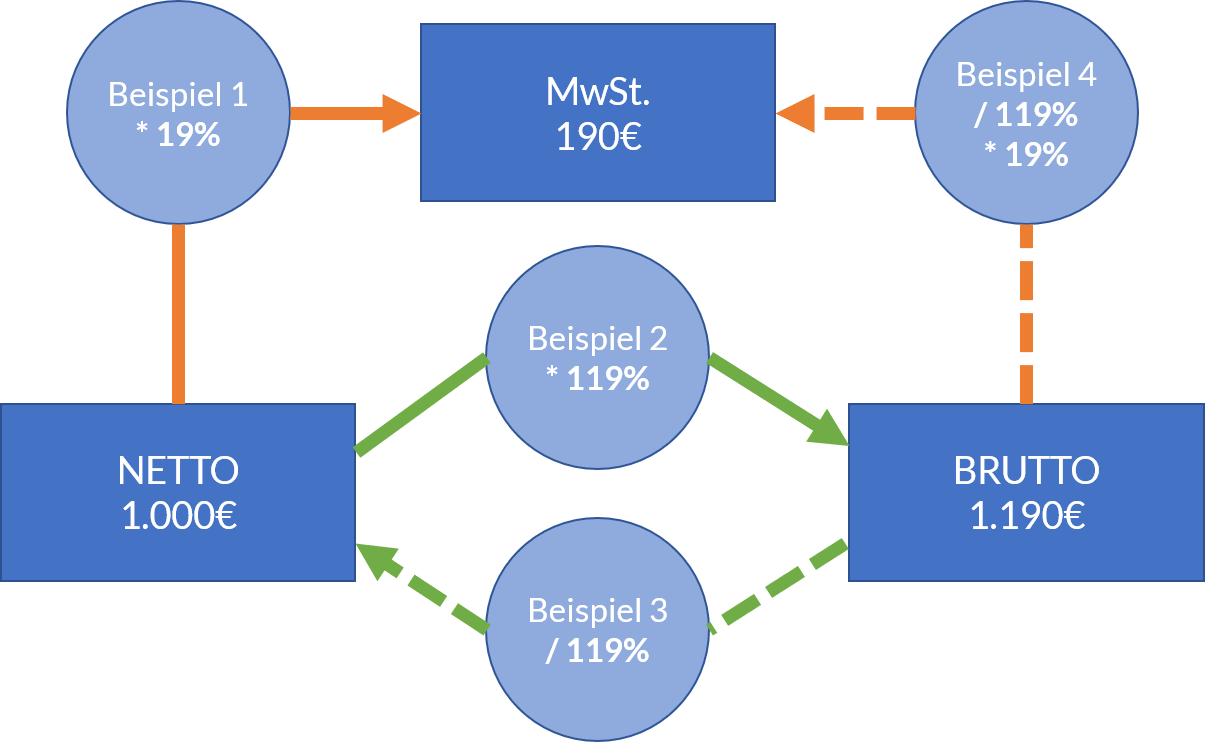
Zu beginn werden die wichtigsten begriffe erläutert und anschließend werden beispiele durchgerechnet. Beim einkaufen ist es für dich hilfreich zu verstehen was ein rabatt aussagt. Unter der prozentrechnung versteht man das rechnen mit prozenten. Davor ist es jedoch sinnvoll die gleichungen und begriffe zur prozentrechnung einmal kurz zu behandeln.
Wir sehen uns dazu gleich einige beispiele an. Aufgaben zur prozentrechnung lassen sich auf unterschiedliche weisen lösen. Erklärung formeln prozentrechnung in der prozentrechnung gibt es eine reihe an grundformeln für die berechnung der einzelnen angaben. Unter anderem bei krediten oder geldanlagen begegnet dir die prozentrechnung.
Grundwert prozentsatz und prozentwert prozentangaben werden verwendet um anteile an etwas ganzem anzugeben. Ob im beruf oder im alltag.








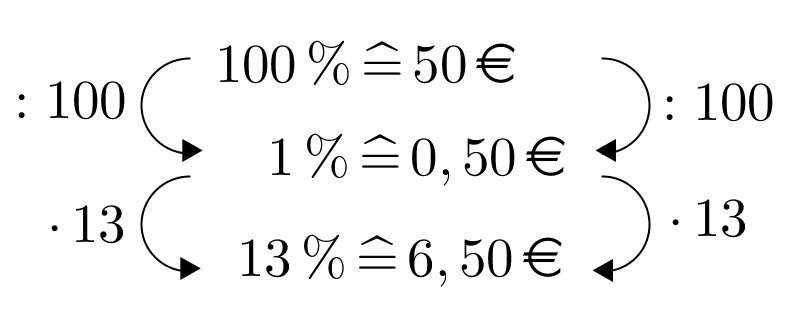
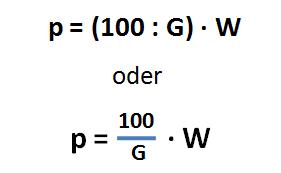


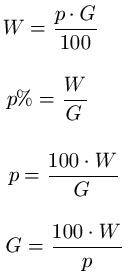







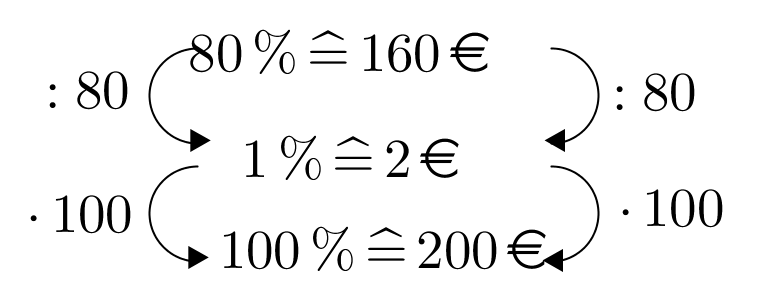













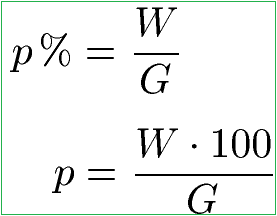

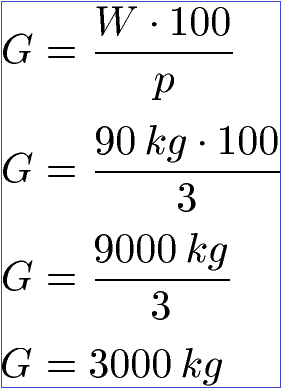

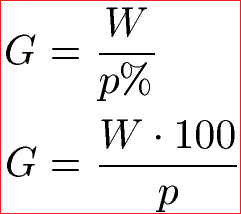

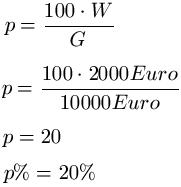

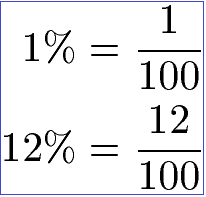

:fill(000,true):no_upscale()/praxistipps.s3.amazonaws.com%2Fexcel-mit-prozenten-rechnen_537814cd.png)